1648. Функция Фенвика

Значением функции Фенвика для числа n называется максимальная степень двойки, на которую нацело делится число n. По заданному числу n определите для него значение функции Фенвика.

Вход. Одно число n (0 < n ≤ 2³¹ – 1).

Выход. Выведите значение функции Фенвика для числа n.

Пример входа

12

Пример выхода

4

РЕШЕНИЕ

элементарная задача – битовые операции

Анализ алгоритма

Пока значение четное, будем его делить на 2, подсчитывая количество делений k. Значение 2^k и будет максимальной степенью двойки, на которую нацело делится исходное число n.

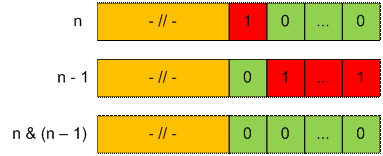
Задачу также можно решить без использования циклов. Операция n & (n – 1) уничтожает в числе n последнюю единицу в бинарном представлении. Значение n – (n & (n – 1)) будет искомым.

Реализация алгоритма

Читаем входное значение n.

scanf("%d",&n);

Пока число n делится на 2 (последний бит n равен нулю), делим n на 2 (совершаем битовый сдвиг на одну позицию вправо) и увеличиваем искомую степень двойки k на единицу.

while(!(n & 1))

n >>= 1, k++;

Выводим ответ.

printf("%d\n",1 << k);

Реализация без использования цикла

scanf("%d",&n);

res = n - (n & (n - 1));

printf("%d\n",res);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int res = n - (n & (n - 1));

System.out.println(res);

}

}